카테고리, 댓글/답글과 같은 계층(트리) 데이터베이스 구조 설계 및 개선하기

카테고리와 같은 계층형 데이터 구조는 어떻게 설계하고 관리해야 할까?

현재 운영하고 있는 사이트에서는 아래 사진과 같이 하나의 카테고리가 있으면 parent_id 컬럼을 이용해 부모-자식 관계를 표현하고 있다. 이 방식을 인접 목록(Adjacency List) 방식이라고 한다.

문제 상황

그러나 프로젝트에서 사용되고 있는 카테고리 목록 조회 API의 본래 요구사항은 현재 카테고리를 기준으로 모든 하위 카테고리를 가져올 수 있어야 한다였으나 현재 스키마 설계로는 조회하고 싶은 카테고리의 가장 마지막 노드(가장 마지막 하위 카테고리)를 parent_id를 통해 몇 번을 조인해서 가져올 수 있는지 알 수 없는 구조였다. 그래서 우선은 재귀 쿼리를 사용해 children 응답 컬럼을 추가하여 모든 하위 카테고리 정보를 가져오도록 했다.

재귀 쿼리를 사용해 모든 하위 카테고리 아이디들을 가져왔으나, 쿼리 자체의 복잡도가 높았고 깊이가 깊을수록 실행 시 부담이 있을 터였다. 또한 이 상태로는 어드민 입장에서 트리 구조가 한 번에 파악이 어렵기 때문에 새로운 카테고리를 등록하려고 할 때 어떤 카테고리를 부모로 둘 지 직접 아이디를 찾아야 한다는 번거로움이 있었다.

해결 방안

계층 구조의 대표적인 패턴은 총 4가지가 있다.

각 패턴의 동작 방식을 아래의 데이터를 이용해 각 항목들을 조회/실행하는 쿼리를 짜보며 살펴보자.

* 데이터베이스는 MySQL을 사용하고 있습니다.

1. 자식 조회: 현재 카테고리의 자식 카테고리 조회하기
2. 트리 조회: 현재 카테고리의 모든 하위 카테고리 조회
3. 이동, 삽입, 삭제

1. 인접 목록

categories

* id (PK)

* name

parent_id (FK)

원래 내가 구현했던 카테고리 스키마 구조이다. 위에 보이는 것과 같이 parent_id를 추가하여 관리한다.

a. 자식 조회

(4)소파의 자식 조회를 해보자. parent_id만 알고 있으면 쉽게 찾아올 수 있다.

 SELECT *
FROM categories
WHERE parent_id = 4
 
# 실행 결과 - [(7)1인 소파, (8)다인용 소파]

b. 트리 조회

그렇다면 모든 하위 카테고리를 가져오는(트리 조회) 쿼리를 짜보자.

 SELECT *
FROM categories c1
         LEFT JOIN categories c2 ON c1.id = c2.parent_id
         LEFT JOIN categories c3 ON c2.id = c3.parent_id
         ...

도대체 조인을 몇 번을 해야 할까..? 아까 위에서 봤던 것처럼 마지막 노드가 몇 번을 조회해야 나오는지 파악이 불가능하다.

그래서 현재 테이블 구조에서 트리 조회를 하려면 아래와 같이 재귀 쿼리를 통해 찾아올 수 있다. 이번엔 (1)가구의 트리 조회를 해보자.

 WITH RECURSIVE t3 (id, name) AS (SELECT t1.id, t1.name
                                 FROM categories t1
                                 WHERE t1.parent_id = 1
                                 UNION ALL
                                 SELECT t2.id, t2.name
                                 FROM categories t2
                                          INNER JOIN t3 ON t2.parent_id = t3.id)
SELECT *
FROM t3
 
# 실행 결과 - [(3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]

만약 카테고리 테이블의 대량의 데이터가 있다면 반복적인 쿼리를 계속 수행하는 것이므로 메모리 사용량 증가 및 데이터베이스 서버에 부하를 줄 수 있다.

c. 이동, 삽입, 삭제

카테고리 이동과 삽입은 그저 부모 카테고리의 아이디만 알고 있으면 되므로 쉬운 편이다.

그렇지만 삭제는 다르다. parent_id는 FK이기 때문에 하나의 카테고리 삭제하고 싶을 경우, 하위에 달려있는 카테고리들을 단계별로 추적하여 삭제해주어야 하는 번거로움이 있다.

2. 경로 열거

categories

* id (PK)

* name

* path ex) 1/2/3

parent_id 대신 path 컬럼이 추가가 된다. 이 컬럼에는 우리가 아는 디렉터리 구조(ex. /hanna/Desktop)처럼 '/'와 같은 구분자로 path를 저장한다. path는 루트부터 현재 로우의 아이디까지를 나열한다. 가구 카테고리를 추가한다고 치면 { id: 1, name: '가구', path: '1/' } 이런 식으로 추가해 주면 된다.

a. 자식 조회

(4)소파의 자식 조회를 해보자.

 SELECT *
FROM categories
WHERE path LIKE '1/4/_/'
 
# 실행 결과 - [(7)1인 소파, (8)다인용 소파]

b. 트리 조회

(1)가구의 트리 조회를 해보자

 # 나 자신을 포함한 트리 조회
SELECT *
FROM categories
WHERE path LIKE '1/%'
 
# 실행 결과 - [(1)가구, (3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]
 
 
# 나 자신을 제외한 트리 조회
SELECT *
FROM categories
WHERE SUBSTRING(path, 1, LENGTH(path) - 1) LIKE '1/%'
 
# 실행 결과 - [(1)가구, (3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]

c. 이동, 삽입, 삭제

이동과 삽입은 부모가 가지고 있는 path에 내 아이디만 추가로 붙이면 되므로 쉬운 편이다.

path는 그냥 문자열 타입의 컬럼이므로 삭제 자체 또한 쉽다.

그러나 이동/삽입/삭제 시 하위 카테고리들의 path를 모두 수정해 주어야 한다는 번거로움이 조금 있다. 그리고 path 컬럼 자체는 올바른 경로를 작성하도록 강제하기는 힘들기 때문에 유지 비용이 비교적 높을 수 있다.

3. 중첩 집합

categories

* id (PK)

* name

* left

* right

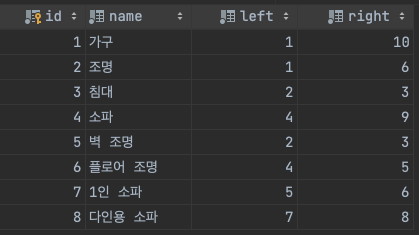
중첩 집합은 자식의 데이터를 가지고 있는 구조이다. 새롭게 left, right 컬럼이 추가된 것을 볼 수 있는데 이 값으로 부모-자식 카테고리를 탐색한다. left와 right 값은 깊이 우선 탐색을 하면서 할당한다. 방법은 다음과 같다.

* 1부터 값을 증가시키면서 진행한다.

1. 현재 위치에서 left에 값을 할당한다.

2. 하위 노드가 있으면 계속 내려가면서 left에 값을 할당한다.

3. 더 이상 내려갈 하위 노드가 없으면 상위 노드로 올라가면서 right에 값을 할당한다.

4. 형제 노드가 있으면 형제 노드로 이동한다.

5. 반복

left, right 값을 모두 할당 후 트리를 보면 값의 크기가

부모 카테고리의 left < 자식 카테고리의 left < 자식 카테고리의 right < 부모 카테고리의 right

로 구성되어 있음을 알 수 있다.

a. 자식 조회

지금까지와 달리 중첩 집합 패턴에서는 자식 조회에는 어려움이 있다. 처음에 나는 left, right 차가 제일 적은 걸 가져오면 되지 않나? 싶었지만 싶지만 중첩 집합 패턴에선 left, right 크기 비교로만 하위 카테고리들을 조회하기 때문에 다른 관계없는 카테고리에서 차가 제일 적은 값을 가지고 있을 수도 있게 된다면 정확한 데이터 조회가 힘들다.

b. 트리 조회

그래도 다행히 트리 조회는 쉬운 편이다. (1)가구의 트리 조회를 해보자.

 # 나 자신을 포함한 트리 조회
SELECT c2.*
FROM categories c1
         JOIN categories c2 ON c2.`left` BETWEEN c1.`left` AND c1.`right`
WHERE c1.id = 1
 
# 실행 결과 - [(1)가구, (3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]
 
 
# 나 자신을 제외한 트리 조회
SELECT c2.*
FROM categories c1
         JOIN categories c2 ON c2.`left` BETWEEN c1.`left` AND c1.`right`
WHERE c1.id = 1
  AND c1.`left` <> c2.`left`
  
# 실행 결과 - [(3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]

(참고) 반대로 나 자신을 포함한 부모 카테고리들을 가져오는 쿼리는 아래와 같다.

join시 on 절에 c1, c2 위치만 변경해 주면 된다.

 SELECT c2.*
FROM categories c1
         JOIN categories c2 ON c1.`left` BETWEEN c2.`left` AND c2.`right`
WHERE c1.id = 4
 
# 결과는 [(1)가구, (4)소파]가 나온다.

c. 이동, 삽입, 삭제

카테고리를 하나를 삭제하고 별도의 작업이 없어도 동일하게 동작한다. 이유는 하나를 삭제해도 여전히 left, right 값의 순서는

부모 카테고리의 left < 자식 카테고리의 left < 자식 카테고리의 right < 부모 카테고리의 right 이기 때문에 영향이 없기 때문이다.

아래에 사진을 보면 (4)소파 카테고리 삭제 시 자연스럽게 (1)가구 카테고리의 자식 노드가 된다.

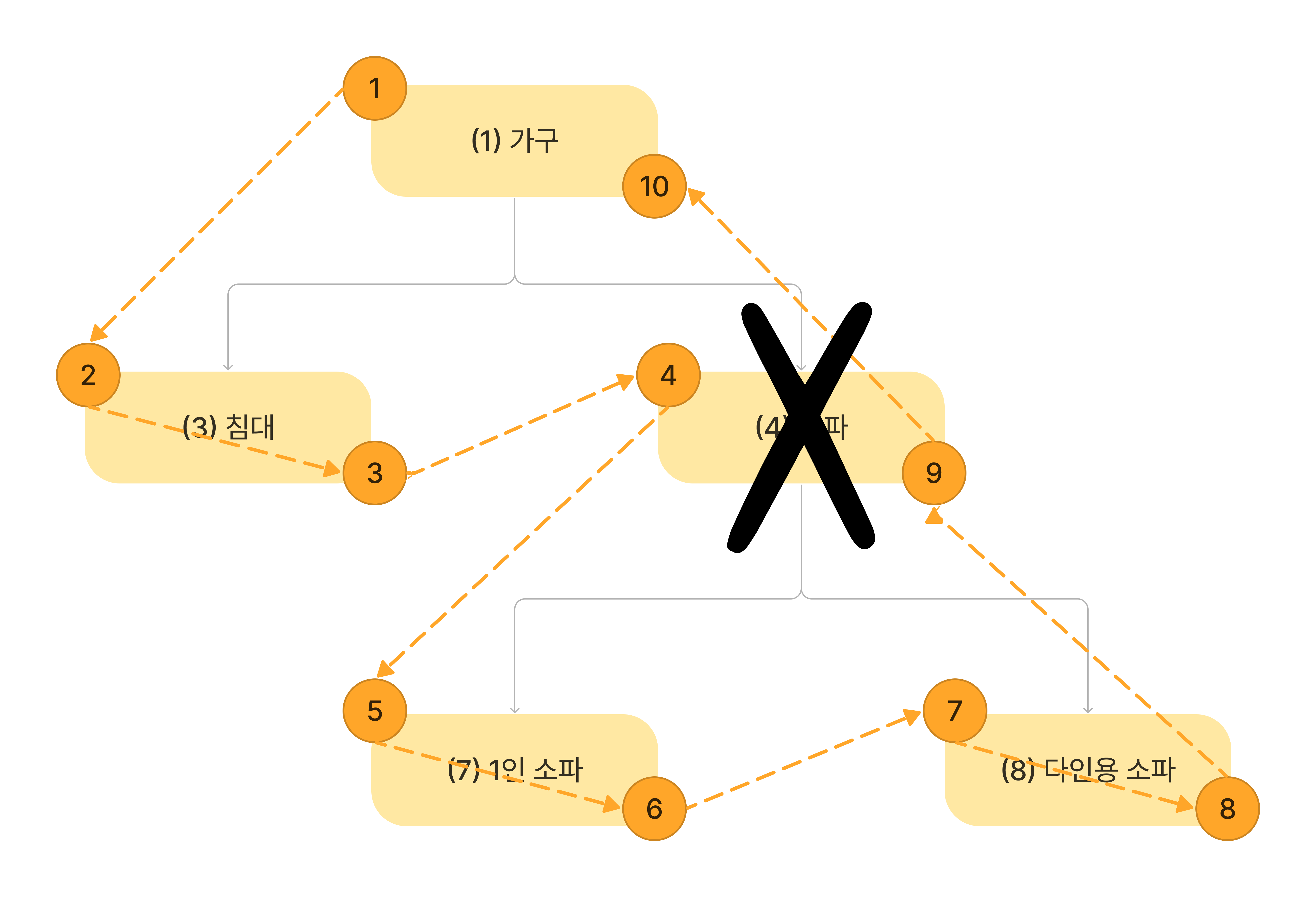
삭제는 쉬운 편이었지만, 예상했다시피 카테고리를 이동, 삽입하는 것은 까다롭다. 새로운 카테고리를 추가/이동하게 되면 left, right의 연산을 다시 해주어야 한다.

그래서 추가와 이동이 빈번할 것 같다면 중첩 집합은 적합하지 않다.

4. 클로저 테이블

categories

* id (PK)

* name

category_paths

* ancestor (PK, FK)

* descendant (PK, FK)

depth

클로저 테이블은 트리의 모든 경로를 저장하는 방식이다. 기존 패턴들과는 다르게 별도의 테이블이 한 개 더 필요하다.

데이터는 아래와 같이 자기 자신 참조부터 모든 부모/자식 관계를 넣어준다. (1)가구 트리를 기준으로 데이터를 삽입해 보았다.

바로 밑 자식만 조회하는 로직이 필요하다면 depth 컬러도 추가해 주도록 하자.

a. 자식 조회

(1)가구의 자식 조회 쿼리는 다음과 같다.

 SELECT c.*
FROM categories AS c
         JOIN category_paths AS p
              ON c.id = p.descendant
WHERE p.ancestor = 1
  AND p.depth = 1;
  
# 실행 결과 - [(3)침대, (4)소파]

b. 트리 조회

트리 조회는 자식 조회 쿼리에서 depth 조건문만 제거해 주면 된다.

 SELECT c.*
FROM categories AS c
         JOIN category_paths AS p
              ON c.id = p.descendant
WHERE p.ancestor = 1;
 
# 실행 결과 - [(1)가구, (3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]

물론 자기 자신을 제외하고 싶다면 where절에 p.descendant = 1 조건을 추가해 주면 되겠다.

c. 이동, 삽입, 삭제

(4)소파 카테고리에 (9)모듈형 소파를 새로 추가하겠다면 쿼리는 아래와같다.

자기 자신 참조를 추가해 주고, 부모의 조상(ancestor)들을 복제해 descendant에 자시 자신 아이디를 넣고 insert 해주면 된다.

 # 삽입
 
INSERT INTO categories (id, name)
VALUES (9, '모듈형 소파')
 
INSERT INTO category_paths (ancestor, descendant)
SELECT ancestor, 9 # 소파의 상위 path 모두 가져오기
FROM category_paths
WHERE descendant = 4
UNION ALL
SELECT 9, 9 # 자기 자신 참조

삭제 쿼리는 아래와 같다. 아래의 쿼리를 사용해 path 테이블에서 경로를 모두 제거해 준다.

 # 소파 카테고리 삭제
DELETE
FROM category_paths
WHERE descendant = 4;

 # 소파 카테고리의 트리 삭제
DELETE
FROM category_paths
where descendant IN (SELECT descendant
                     FROM category_paths
                     WHERE ancestor = 4);

그러고 나서 category테이블에서도 삭제하려는 카테고리의 데이터를 삭제해 주는 것도 잊지 말자!

이동 또한 경로를 제거해 주고 위의 쿼리를 통해 insert만 해주면 되므로 쉽다.

그런데 만약 depth를 별도로 사용해주고 있다면, 당연히 트리 전체에 depth는 재계산이 필요하다 🥹

정리

지금까지 각 패턴의 동작방식에 대해 살펴보았다. 아래 표를 통해 장/단점을 한눈에 봐보자.

패턴	테이블	자식 조회	트리 조회	이동	삽입	삭제	참조 정합성
인접 목록	1	쉬움	어려움	쉬움	쉬움	쉬움	가능
경로 열거	1	쉬움	쉬움	쉬움	쉬움	쉬움	불가능
중첩 집합	1	어려움	쉬움	어려움	어려움	어려움	불가능
클로저 테이블	2	쉬움	쉬움	쉬움	쉬움	쉬움	가능

해결

최종적으로 나는 카테고리 테이블 구조를 클로저 테이블로 재구성하였다. 이유는 자식 조회, 트리 조회가 모두 유연하길 원했기 때문이다.

참고로 현재 프로젝트에서는 TypeORM을 사용 중인데, TypeORM에서 계층 구조에 대한 메서드를 제공해주고 있다. 문서를 참고하면 손쉽게 적용이 가능하다.

참고

Models for hierarchical data

책 <<SQL AntiPatterns>>

'Database' 카테고리의 다른 글

[MySQL] 탐색할 컬럼에 분명 인덱스를 걸었는데, 슬로우 쿼리?! (묵시적 형 변환) (0)	2023.04.08

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

annahxxl

카테고리, 댓글/답글과 같은 계층(트리) 데이터베이스 구조 설계 및 개선하기

문제 상황

해결 방안

정리

해결

참고

'Database' 카테고리의 다른 글

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역

	SELECT *
	FROM categories
	WHERE parent_id = 4

	# 실행 결과 - [(7)1인 소파, (8)다인용 소파]

	SELECT *
	FROM categories c1
	LEFT JOIN categories c2 ON c1.id = c2.parent_id
	LEFT JOIN categories c3 ON c2.id = c3.parent_id
	...

	WITH RECURSIVE t3 (id, name) AS (SELECT t1.id, t1.name
	FROM categories t1
	WHERE t1.parent_id = 1
	UNION ALL
	SELECT t2.id, t2.name
	FROM categories t2
	INNER JOIN t3 ON t2.parent_id = t3.id)
	SELECT *
	FROM t3

	# 실행 결과 - [(3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]

	SELECT *
	FROM categories
	WHERE path LIKE '1/4/_/'

	# 실행 결과 - [(7)1인 소파, (8)다인용 소파]

	# 나 자신을 포함한 트리 조회
	SELECT *
	FROM categories
	WHERE path LIKE '1/%'

	# 실행 결과 - [(1)가구, (3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]


	# 나 자신을 제외한 트리 조회
	SELECT *
	FROM categories
	WHERE SUBSTRING(path, 1, LENGTH(path) - 1) LIKE '1/%'

	# 실행 결과 - [(1)가구, (3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]

	# 나 자신을 포함한 트리 조회
	SELECT c2.*
	FROM categories c1
	JOIN categories c2 ON c2.`left` BETWEEN c1.`left` AND c1.`right`
	WHERE c1.id = 1

	# 실행 결과 - [(1)가구, (3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]


	# 나 자신을 제외한 트리 조회
	SELECT c2.*
	FROM categories c1
	JOIN categories c2 ON c2.`left` BETWEEN c1.`left` AND c1.`right`
	WHERE c1.id = 1
	AND c1.`left` <> c2.`left`

	# 실행 결과 - [(3)침대, (4)소파, (7)1인 소파, (8)다인용 소파]

	SELECT c2.*
	FROM categories c1
	JOIN categories c2 ON c1.`left` BETWEEN c2.`left` AND c2.`right`
	WHERE c1.id = 4

	# 결과는 [(1)가구, (4)소파]가 나온다.

	SELECT c.*
	FROM categories AS c
	JOIN category_paths AS p
	ON c.id = p.descendant
	WHERE p.ancestor = 1
	AND p.depth = 1;

	# 실행 결과 - [(3)침대, (4)소파]

	# 삽입

	INSERT INTO categories (id, name)
	VALUES (9, '모듈형 소파')

	INSERT INTO category_paths (ancestor, descendant)
	SELECT ancestor, 9 # 소파의 상위 path 모두 가져오기
	FROM category_paths
	WHERE descendant = 4
	UNION ALL
	SELECT 9, 9 # 자기 자신 참조

	# 소파 카테고리 삭제
	DELETE
	FROM category_paths
	WHERE descendant = 4;

	# 소파 카테고리의 트리 삭제
	DELETE
	FROM category_paths
	where descendant IN (SELECT descendant
	FROM category_paths
	WHERE ancestor = 4);

카테고리, 댓글/답글과 같은 계층(트리) 데이터베이스 구조 설계 및 개선하기

문제 상황

해결 방안

정리

해결

참고

'Database' 카테고리의 다른 글

'Database' Related Articles

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역